Sunday, October 9, 2011
Benford's Law and the Decreasing Reliability of Accounting Data for US Firms
A few months ago I came upon an old episode of Radiolab, one of my favorite podcasts whose host Jad Abumrad just won a Macarthur Fellowship. The episode was about numbers. It made me nostalgic for my youthful enthrallment with the pristine world of mathematics, before I succumbed to the gritty reality of the financial world. Among the episode's astounding revelations was that babies count on a logarithmic scale.
A second earth-shattering fact is that there are more numbers in the universe that begin with the digit 1 than 2, or 3, or 4, or 5, or 6, or 7, or 8, or 9. And more numbers that begin with 2 than 3, or 4, and so on. This relationship holds for the lengths of rivers, the populations of cities, molecular weights of chemicals, and any number of other categories. What a blow to any of us who purport to have mastered the basic facts of the world around us!
This numerical regularity is known as Benford's Law, and specifically, it says that the probability of the first digit from a set of numbers is d is given by
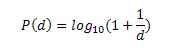
In fact, Benford's law has been used in legal cases to detect corporate fraud, because deviations from the law can indicate that a company's books have been manipulated. Naturally, I was keen to see whether it applies to the large public firms that we commonly study in finance.
I downloaded quarterly accounting data for all firms in Compustat, the most widely-used dataset in corporate finance that contains data on over 20,000 firms from SEC filings. I used a standard set of 43 variables that comprise the basic components of corporate balance sheets and income statements (revenues, expenses, assets, liabilities, etc.).
And lo, it works! Here are the distribution of first digits vs. Benford's law's prediction for total assets and total revenues.
Next, I looked at how adherence to Benford's law changed over time, using a measure of the sum of squared deviations of the empirical density from the Benford's prediction.
where ^P(d) is the empirical probability of the first digit d.
Deviations from Benford's law have increased substantially over time, such that today the empirical distribution of each digit is about 3 percentage points off from what Benford's law would predict. The deviation increased sharply between 1982-1986 before leveling off, then zoomed up again from 1998 to 2002. Notably, the deviation from Benford dropped off very slightly in 2003-2004 after the enactment of Sarbanes-Oxley accounting reform act in 2002, but this was very tiny and the deviation resumed its increase up to an all-time peak in 2009.
So according to Benford's law, accounting statements are getting less and less representative of what's really going on inside of companies. The major reform that was passed after Enron and other major accounting standards barely made a dent.
Next, I looked at Benford's law for three industries: finance, information technology, and manufacturing. The finance industry showed a huge surge in the deviation from Benford's from 1981-82, coincident with two major deregulatory acts that sparked the beginnings of that other big mortgage debacle, the Savings and Loan Crisis. The deviation from Benford's in the finance industry reached a peak in 1988 and then decreased starting in 1993 at the tail end of the S&L fraud wave, not matching its 1988 level until … 2008.
The time series for information technology is similarly tied to that industry's big debacle, the dotcom bubble. Neither manufacturing nor IT showed the huge increase and decline of the deviation from Benford's that finance experienced in the 1980s and early 1990s, further validating the measure since neither industry experienced major fraud scandals during that period. The deviation for IT streaked up between 1998-2002 exactly during the dotcom bubble, and manufacturing experienced a more muted increase during the same period.
While these time series don't prove anything decisively, deviations from Benford's law are compellingly correlated with known financial crises, bubbles, and fraud waves. And overall, the picture looks grim. Accounting data seem to be less and less related to the natural data-generating process that governs everything from rivers to molecules to cities. Since these data form the basis of most of our research in finance, Benford's law casts serious doubt on the reliability of our results. And it's just one more reason for investors to beware.
As noted by William Black in his great book on the S&L crisis The Best Way to Rob a Bank Is to Own One, the most fraudulent S&Ls were the ones that looked most profitable on paper. That was in fact an inherent part of the scam. So perhaps, instead of looking solely at profitability, we should also consider this more fundamental measure of a firm's "performance." And many questions remain. What types of firms, and what kind of executives drive the greatest deviations from Benford's law? Does this measure do well in predicting known instances of fraud? How much of these deviations are driven by government deregulation, changes in accounting standards, and traditional measures of corporate governance?
Stay tuned to find out.





No comments:
Post a Comment